En biologie, l’expérimentateur a souvent un jeu de mesures moyen à grand (100 à 100k lignes, plusieurs colonnes). C’est une matrice de mesures obtenus sur des individus pour un ensemble de paramètres cliniques ou biologiques. Les lignes de cette matrice sont les variables observées : gènes, protéines, pourcentages de types cellulaires… Les colonnes sont les individus. Les individus forment des groupes ayant des caractéristiques différentes : réponse à un médicament, rechute… L’expérimentateur cherche parmi les marqueurs (ie les variables/lignes) ceux qui sont associés au regroupement ou plus généralement à la réponse des individus. Une façon d’aborder la question est de répéter sur chaque marqueur un test statistique classique (test de Student, ANOVA, etc). Ces tests statistiques s’interprétent dans le cadre d’un seuil de p-value de 5%. Ce seuil correspond au risque de se tromper. Lorsque le test est appliqué une fois, le risque est de 5%, soit 1/20. Lorsque le test est répété de multiples fois, le risque est multiplié par le nombre de répétitions. Ainsi, au seuil de 5%, 5% x 1000 marqueurs = 50 tests ou marqueurs seront déclarés statistiquement significatifs par l’effet seul du hasard, ie seulement parce que le risque a été provoqué 1000 au lieu d’une seule fois. Au seuil de 1%, 1% x 1000 marqueurs = 10 tests seront déclarés statistiquement significatifs par l’effet du hasard. Ces marqueurs déclarés statistiquement significatifs par l’effet seul du hasard sont donc des fausses découvertes pour l’expérimentateur. Avec une matrice de mesures de grande taille, l’expérimentateur est confronté au problème des tests multiples. La p-value utilisée classiquement n’est plus un critère pour déclarer intéressant un marqueur. Nous allons simuler un jeu de données pour comprendre ce phénomène, et nous allons voir une méthode graphique pour contrôler le nombres de fausses découvertes.
Jeu de données sans différences
Nous allons étudier un jeu de données simulées. Ce jeu simule 2 groupes de 10 individus et 1000 marqueurs, donc une matrice de 1000 lignes x 20 colonnes. Commençons par définir des données qui ne contiennent pas de réelles différences.
# Synchronisation du generateur de nombre aleatoire
set.seed(1)
# Jeu aleatoire de donnees suivant une loi gaussienne
mat=matrix(rnorm(20*1000),1000,20)
mat2=mat # archivageNous pouvons représenter le jeu de données via une heatmap, une carte de chaleur. L’idée est de transformer les valeurs numériques de la matrice par une couleur afin d’obtenir une image. L’oeil et le cerveau sont plus sensibles et réactifs à une image qu’à une matrice de nombres. Les couleurs par défaut sont difficilement interprétables ; on remplace par une palette de couleurs avec un gradient négatif (Bleu à Blanc) et un gradient positif (Blanc à Rouge).
# heatmap, echelle de couleurs par défaut
image(t(mat)[,rev(seq(nrow(mat)))], axes = F)
# echelle de couleurs en double degrade negatif et positif
image(t(mat)[,rev(seq(nrow(mat)))], axes = F, col = colorRampPalette(c("Blue2", "White", "Red2"))(32))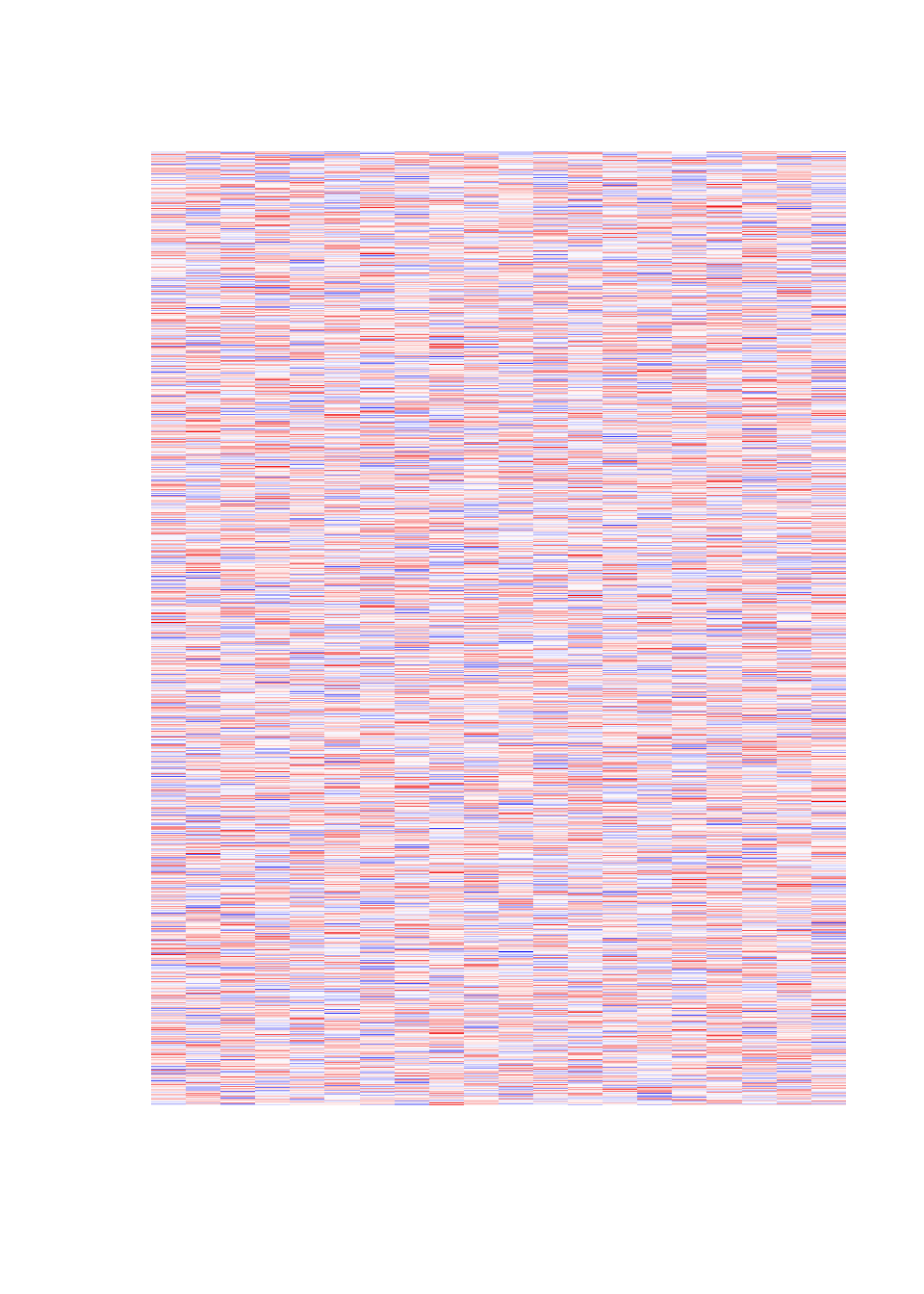
Calcul de score
Nous appliquons une méthode “Brute Force” qui consiste à interroger chaque variable (ligne) de la matrice et à rechercher si elle est corrélée avec le groupement des aptients en 2 groupes, c’est à dire si la vairable montre une différence de moyenne entre les deux groupes. Lorsque le score sera établi sur une ligne, on effectuera une boucle pour calculer le score sur l’ensemble des lignes.
Score sur une ligne
Nous allons définir un score pour déclarer un marqueur intéressant. Le test de Student et sa p-value est un choix classique. Nous voulons effectuer le test sur toutes les lignes de la matrice grâce à une boucle. Pour réaliser le coeur de la boucle, travaillons sur la première ligne pour définir le code R.
# Calcul du test de Student sur la 1ere ligne
res = t.test(mat[1,1:10],mat[1,11:20])
res # affiche le contenu de la variable resultant du test de Student
##
## Welch Two Sample t-test
##
## data: mat[1, 1:10] and mat[1, 11:20]
## t = -0.74448, df = 17.52, p-value = 0.4665
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -1.2818449 0.6120472
## sample estimates:
## mean of x mean of y
## -0.5187188 -0.1838200La structure du résultat permet d’identifier la partie qui nous intéresse.
str(res) # structure du résultat
## List of 9
## $ statistic : Named num -0.744
## ..- attr(*, "names")= chr "t"
## $ parameter : Named num 17.5
## ..- attr(*, "names")= chr "df"
## $ p.value : num 0.466
## $ conf.int : num [1:2] -1.282 0.612
## ..- attr(*, "conf.level")= num 0.95
## $ estimate : Named num [1:2] -0.519 -0.184
## ..- attr(*, "names")= chr [1:2] "mean of x" "mean of y"
## $ null.value : Named num 0
## ..- attr(*, "names")= chr "difference in means"
## $ alternative: chr "two.sided"
## $ method : chr "Welch Two Sample t-test"
## $ data.name : chr "mat[1, 1:10] and mat[1, 11:20]"
## - attr(*, "class")= chr "htest"On extrait la partie du résultat en utilisant le symbole $.
res$p.value # extraction de la p-value
## [1] 0.4664565Boucle de calcul
Maintenant que le code est défini, nous l’insérons dans une boucle. Il existe plusieurs possibilités pour enregistrer le score (ie la p-value) dans un vecteur qui nous permettra ensuite de retenir les marqueurs les plus pertinents. Pour la boucle nous choisissons de pré-définir le vecteur de résultat.
# Boucle pour extraire toutes les p-values
# Version avec accumulation
# vec=NULL
# for(i in 1:nrow(mat)) {
# res2=t.test(mat[i,1:10],mat[i,11:20])
# print(res2$p.value)
# vec=c(vec,res2$p.value)
# }
# vec
# Version avec pre-initilisation
vec = rep(NA, 1000)
# vec = matrix() # version je-me-pose-pas-de-question
for(i in 1:nrow(mat)) {
res2 = t.test(mat[i,1:10], mat[i,11:20])
#print(res2$p.value)
vec[i] = res2$p.value
}On vérifie la variabilité du résultat.
head(vec)
## [1] 0.46645650 0.83996475 0.46990800 0.02188267 0.71253108 0.46391811
tail(vec)
## [1] 0.33568922 0.34935958 0.03896348 0.88552095 0.86810947 0.84155214Analyse du score
Nous avons donc une p-value pour chaque marqueur. Nous allons décrire ce vecteur, numériquement et graphiquement.
# Description numerique et graphique des p-values
summary(vec)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.001928 0.268153 0.484081 0.505745 0.755273 0.999250
hist(vec, nclass = 20, ylim = c(0, 100)) # 1 barre = 0.05
abline(h=50, lw=2, col="red") # la hauteur moyenne des barres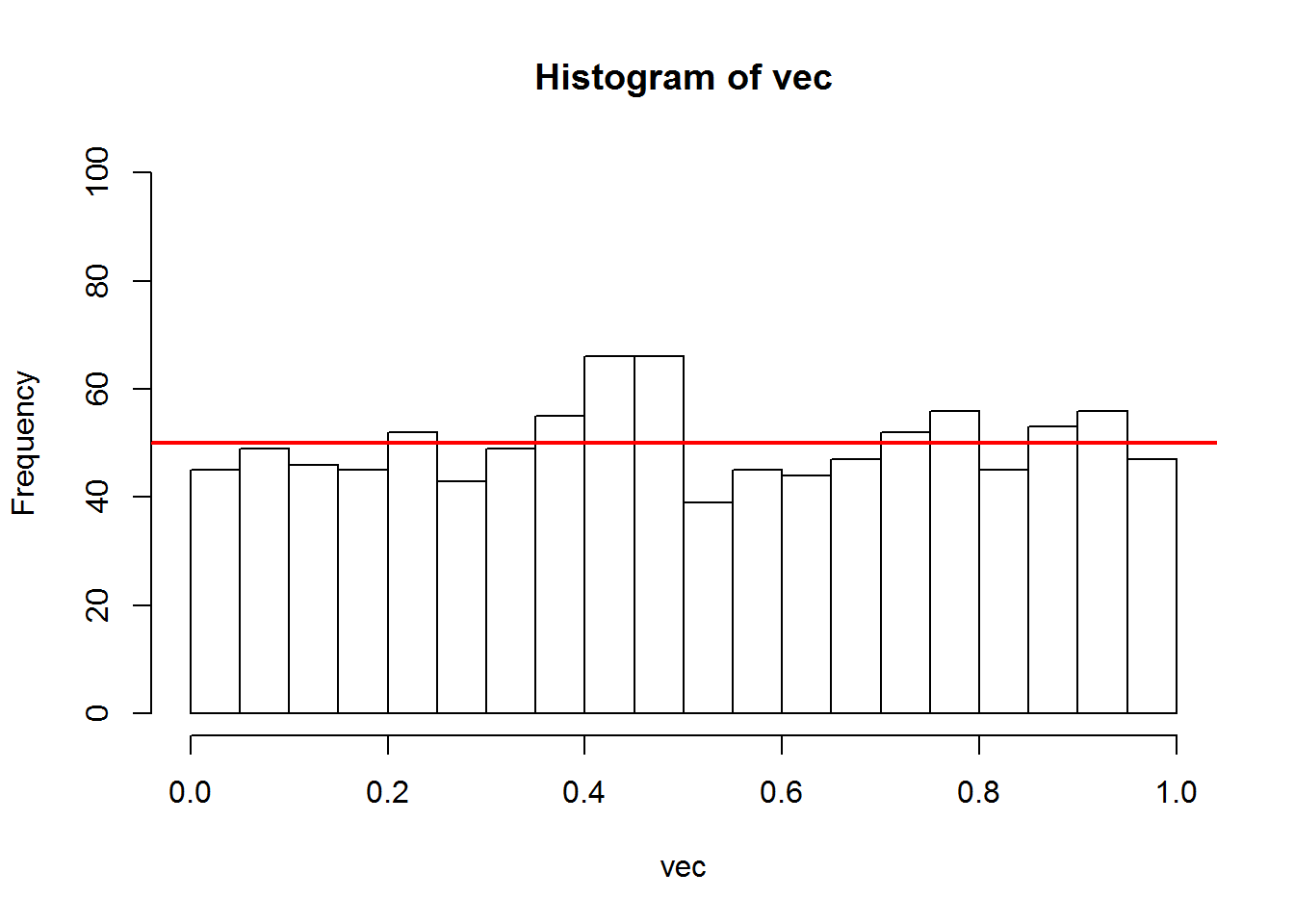
Les valeurs s’étendent de 0 à 1. L’histogramme nous montre que c’est une loi uniforme. Visuellement la moyenne est autour de 50.
En fait, la hauteur moyenne est égale aux nombres de tests multiplié par la largeur de la barre. Les p-values suivent une loi uniforme entre 0 et 1 ou 0% et 100%. L’histogramme est présenté avec des intervalles d’une largeur de 5% (0.05 ou 1/20). Visuellement la moyenne est autour de 50. Cette valeur est logique, elle provient du nombre de tests et de la largeur des barres de l’histogramme : 1000 x 1/20 = 50. Point important, le nombre de tests déclarés statistiquement significatifs au seuil de 5% est de 50, 45 exactement dans le tirage aléatoire que nous avons effectué.
Questions : que se passe-t-il si l’on définit un seuil de significativité à 1% ? Quel est la hauteur moyenne ? Combien de p-value sont dans une tranche de 1% ? Quel est le pourcentage de p-value dans une tranche de 1% ?
Jeu de données avec différences
Ajout d’une différence
Nous allons introduire dans la matrice de données un changement pour le premier groupe. Pour les 100 premiers marqueurs, nous simulons une augmentation de valeur moyenne.
mat3 = mat # recopie intégrale
mat3[1:100, 1:10] = mat[1:100, 1:10] + 2.50 # modification du 1er groupeLa carte de couleurs de ce nouveau jeu de données montre bien la changement introduit.
image(t(mat3)[,rev(seq(nrow(mat)))], axes = F)
Recalcul du score
Refaisons le calcul du score.
# Version avec pre-initilisation
vec3 = rep(NA, 1000)
for(i in 1:nrow(mat3)) {
res2 = t.test(mat3[i,1:10], mat3[i,11:20])
#print(res2$p.value)
vec3[i] = res2$p.value
}Nouvelle analyse
Refaisons la description graphique.
hist(vec3, nclass = 20) # 1 barre = 0.05
# C'est une loi uniforme
abline(h=45, lw=2, col="red") # la hauteur moyenne des barres = 900/20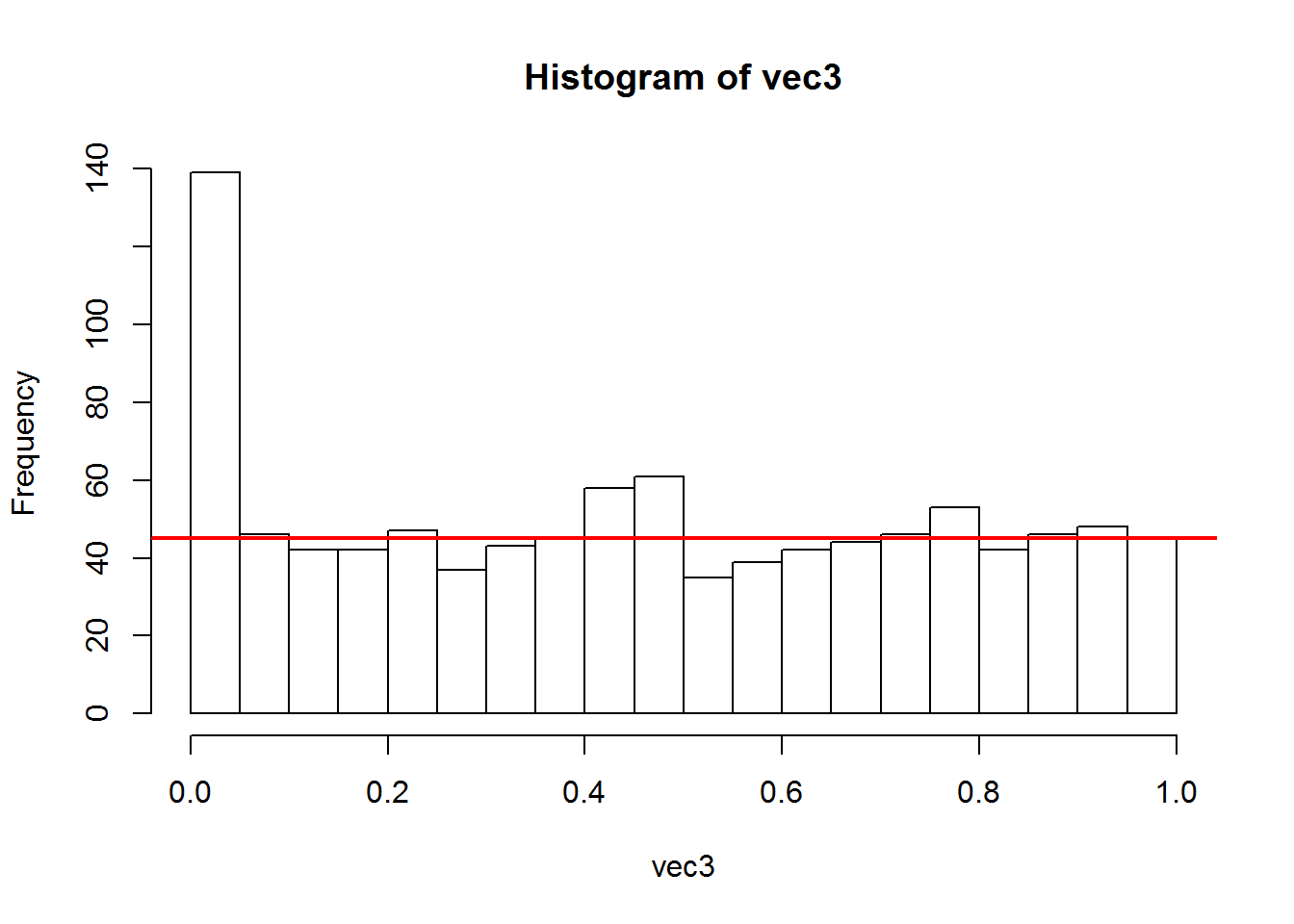
Nous observons à nouveau une loi uniforme dans la moitié droite (p-value > 0.5) et la plus grande partie de l’histogramme. Cependant la différence la plus marquante est dans la première barre de l’histogramme, ie de 0 à 5%. En effet, la quantité de p-value est passée de 45 à 140, soit une augmentation d’environ 100 (95 exactement dans cette réalisation aléatoire).
La hauteur moyenne des barres est de 45 dans la partie droite de l’histogramme.
Donc pour un seuil classique de p-value à 5%, il y a 139 tests déclarés statistiquement significatifs. Cependant, à cause des tests multiples effectués, une partie de ces 139 marqueurs sont des fausses découvertes. Nous pouvons cette quantité en observant la partie droite de l’histogramme. Graphiquement et numériquement, nous estimons le nombre de fausses découvertes à 45 dans un intervalle de 5%. Donc sur les 139 tests déclarés statistiquement significatifs, 45 sont des fausses découvertes. On utilise comme critère le taux de fausses découvertes. C’est le nombre de fausses découvertes divisé par le nombre de découvertes. Le terme anglais est False Discovery Rate. Ici le taux est de 45 / 139, soit environ 1/3.
count = table(cut(vec3, breaks = seq(0, 1, 0.05)))
count
##
## (0,0.05] (0.05,0.1] (0.1,0.15] (0.15,0.2] (0.2,0.25] (0.25,0.3]
## 139 46 42 42 47 37
## (0.3,0.35] (0.35,0.4] (0.4,0.45] (0.45,0.5] (0.5,0.55] (0.55,0.6]
## 43 45 58 61 35 39
## (0.6,0.65] (0.65,0.7] (0.7,0.75] (0.75,0.8] (0.8,0.85] (0.85,0.9]
## 42 44 46 53 42 46
## (0.9,0.95] (0.95,1]
## 48 45
mean(count[5:20])
## [1] 45.6875Si l’on souhaite diminuer ce taux, on se placera à un seuil de p-value plus faible. Prenons par exemple 1%. Ici l’estimation dans la partie droite donne 10 fausses découvertes en moyenne dans un intervalle de 1%. Le nombre de fausses découvertes est en moyenne de 10. Le premier intervalle de 0 à 1% totalise environ 110 découvertes. Donc le taux de fausses découvertes n’est plus que de 10 / 110, soit 1/10. C’est très nettement inférieur et fera perdre moins de temps à l’expérimentateur lors de la validation.
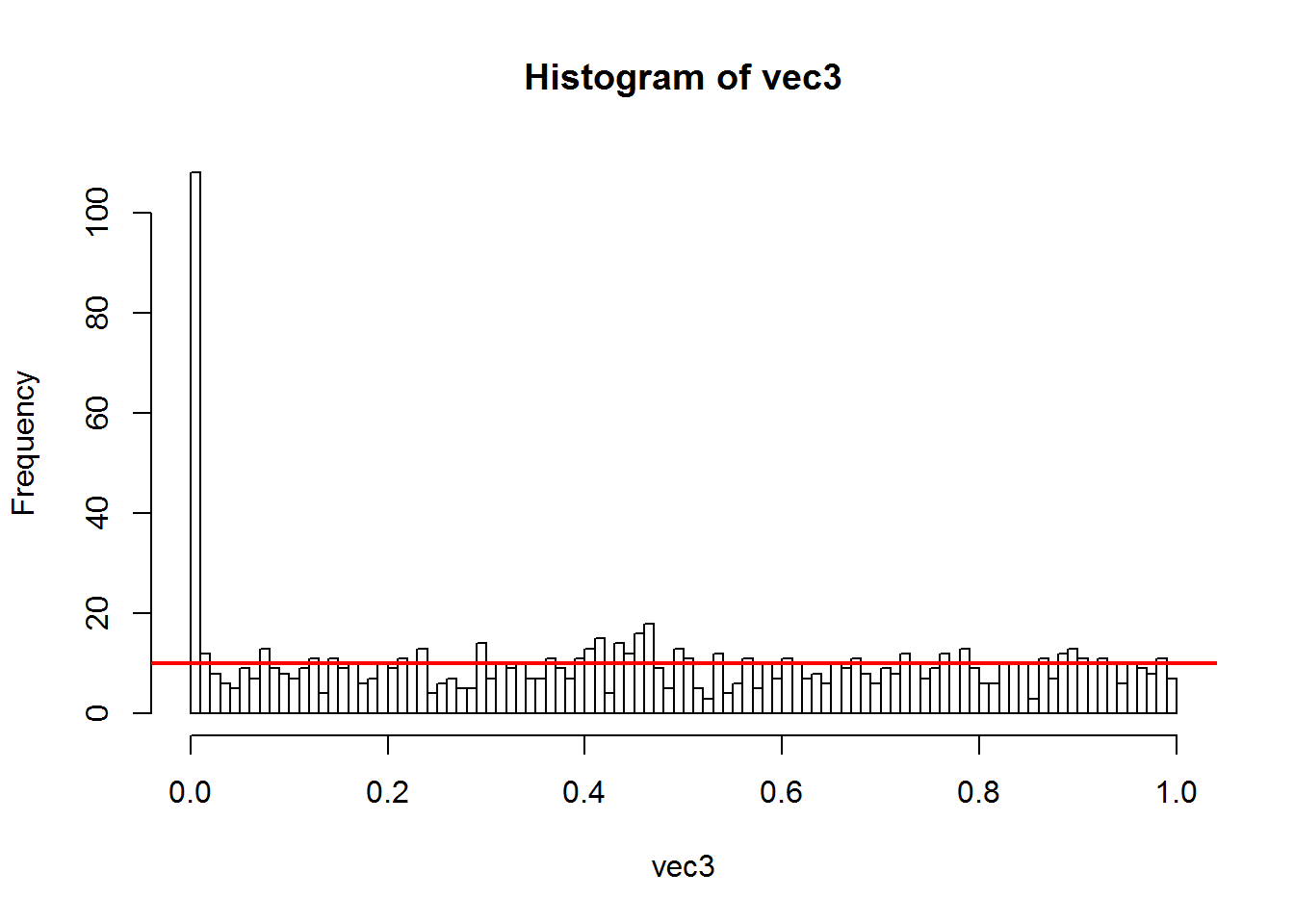
hist(vec3, nclass = 100) # 1 barre = 0.05
# C'est une loi uniforme
abline(h=1000/100, lw=2, col="red") # la hauteur moyenne des barres